XVI.1 PENDAHULUAN

BAB XVI
METODA PERMUKAAN RESPON

XVI.1 PENDAHULUAN

Dalam Bab VII, Bag. VII.2 diuraikan seperlunya tentang regresi linear sedangkan regresi lengkung dalam Bag. VII.3 untuk sebuah variabel bebas atau variabel prediktor. Contoh untuk regre­si linear yang diberikan dalam Bag. VII. 2 adalah Y_x = 17,921 + 1,073 X_j dengan pengertian X menyatakan waktu lamanya meng­aduk larutan sedangkan Y endapan zat yang terjadi. Regresi leng­kung dalam Bag. VII.3 adalah Y_x = - 73,16 + 5,79 - 0,09 dengan X menyatakan temperatur dan Y pengembangan volume zat pada temperatur X.

Model-model regresi seperti di atas dicari berdasarkan data hasil penelitian menggunakan metoda kuadrat terkecil. Kita tabu (lihat kembali Bag. VII.2 dan VII.3, Bab VII) bahwa Y merupakan respon daripada X, yang berarti terjadinya Y (sebagian atau selu­ruhnya) dikarenakan oleh X. Secara matematik dikatakan bahwa Y fungsi dari X, ditulis Y = f (X). Jika fungsi ini digambarkan gra­fiknya dalam bidang dengan sumbu X tegaklurus sumbu Y, terjadi­lah garis; lurus atau linear jika X dalam posisi linear berpangkat satu, lengkung jika X tidak demikian. Dalam contoh di atas, yang pertama berbentuk linear sedangkan yang terakhir merupakan parabola. Karena Y merupakan respon dari X dan grafiknya beru­pa garis (lurus atau lengkung), dapatlah dikatakan bahwa garis regresi ini sebagai garis respon dengan bentuk umum Y = f (X).

Pemikiran ini dikembangkan untuk model respon Y apabila prediktornya lebih dari satu di bawah sebutan permukaan res­pon.

Hal inilah, secara sederhana akan diperkenalkan dalam bab ini.

XVI.2 BENTUK UMUM PERMUKAAN RESPON

Perhatikan suatu eksperimen yang melibatkan k buah faktor (selanjutnya di sini disebut variabel bebas, prediktor atau kadang-­kadang juga variabel kontrol) X₁, X₂, . - - , X_k dengan Y (disebut juga variabel terikat, variabel tak bebas atau variabel respon). Untuk semua variabel ini yang dapat diukur dan diketahui atau barangkali diduga bahwa Y sebagian atau seluruhnva merupakan respon dari X₁, , X₂, . . . , X_k, maka dikatakan bahwa Y fungsi dari X₁, , X₂, . . . , X_k, dan secara umum ditulis dalam bentuk Y = f (X₁, , X₂, . . . , X_k,). Inilah yang selanjutnya di sini akan disebut sebagai permukaan respon. (Untuk k = 1, diperoleh Y = f(X₁, ) atau cukup ditulis Y = f(X), merupakan garis respon).

Permukaan respon ini, secara grafik dapat digambarkan dalam ruang berdimensi (k + 1), suatu ruang yang sukar dilukiskan dan barangkali hanya bisa dibayangkan. Untuk k = 2 misalnya, dan jika X₁, menyatakan waktu lamanya mengaduk dan X₂, menya­takan temperatur waktu mengaduk sedangkan Y hasil proses kimia menggunakan kedua kegiatan tadi (X₁, dan X₂,) maka se­cara umum diperoleh permukaan respon Y = f(X₁, ,X₂, ). Grafiknya dapat dilukiskan dalam ruang berdimensi tiga dengan mengambil absis X­₁, ordinat X₂ dan sumbu Y tegaklurus pada bidang X₁, X₂,. Hasilnya, suatu permukaan di ruang berdimensi tiga yang sulit digambarkan pada kertas (ruang berdimensi dua). Karena untuk pembahasan akan membantu banyak apabila permukaan respon itu digambarkan, maka kita buat gambar atau grafik dengan cara berikut.

Kita ambil permukaan respon Y = f(X₁, X₂ ), respon Y karena prediktor X₁, dan X₂. Bayangkan bahwa Y = f(X₁, X₂) bentuk­nya telah digambarkan dalam ruang berdimensi tiga. Bentuk ini kita potong oleh bidang datar, sejajar dengan bidang X₁, X₂ Pa­da bidang potong itu terjadi lengkungan (tertutup, terbuka atau terputus-putus bergantung pada bentuk Y = f(X₁, X₂) asalnya), disebut kontur. Kontur inilah yang membantu dalam pembahas­an tentang permukaan respon.

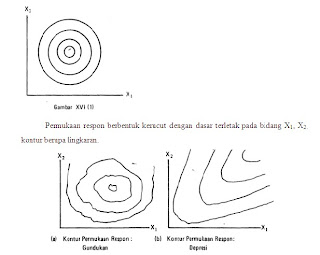
Dijelaskan dengan cara lain, kontur terbentuk jika titik-titik un­tuk semua harga Y yang sama untuk tiap pasang harga X₁, dan X₂, dihubungkan. Tentu saja, jika bidang potong yang sejajar bidang X₁, X₂ dibuat lebih dari satu, kita akan memperoleh kontur-kontur dan melalui kontur-kontur inilah bentuk Y = f(X₁, X₂) di ruang berdimensi tiga dapat dibayangkan. Sebagai contoh, jika kontur-kontur ini berupa lingkaran makin lama makin kecil sedangkan pusatnya sama, maka bentuk Y = f(X₁, X₂) di ruang berdimensi tiga adalah kerucut yang dasarnya terletak pada bidang X₁, X₂ Lihat Gambar XVI (1).

Mudah dimengerti kiranya bahwa bentuk permukaan respon Y = f(X₁, X₂) di ruang berdimensi tiga tidak sebaik contoh di atas, tetapi bisa macam-macam, sehingga konturnya pun macam-macam. Beberapa diantaranya seperti tampak di bawah ini.

XVI.3 KEGUNAAN PERMUKAAN RESPON

Telah dikatakan bahwa kontur-kontur membantu pembahasan permukaan respon lebih mudah untuk eksperimen yang, menye­babkan permukaan respon terjadi. Secara lebih terinci, kegunaan permukaan respon dalam eksperimen adalah

1. Untuk menentukan, berdasarkan sebuah eksperimen, arah eksperimen berikutnya ke titik optimum.

2. Setelah ditemukan optimum atau hampir optimum pada per­mukaan respon, menentukan persamaan permukaan respon di sekitar titik optimum ini.

Salah satu cara untuk mencari titik optimum pada permukaan respon, digunakan cara satu faktor - satu faktor. jika X₂ tetap se­dangkan X₁ berubah-ubah, kita cari X₁ yang membuat Y optimum atau hampir optimum pada harga X₂ tetap itu. Setelah ditemukan harga X₁ eksperimen dapat dilakukan pada X₁ ini dan X₂ yang menyebabkan respon menjadi optimum dapat kita tentukan.

Cara ini sayang tidak selalu berhasil, bergantung pada bentuk permukaan respon; ditambah lagi kenyataan bahwa bentuk permu­kaan respon suatu eksperimen biasanya tidak diketahui.

XV I.4. METODA LINTAS PENDAKIAN TERCURAM

Untuk mengatasi kesulitan disebutkan di atas, orang lalu meng­gunakan metoda lintas pendakian tercuram. Dasar kerjanya adalah melakukan sebuah eksperimen yang sederhana, pada bagian permu­kaan respon yang luasnya kecil, yang untuk praktisnya bisa di­anggap bidang. Kemudian kita tentukan persamaan bidang ini dan lalu setelah itu eksperimen harus diambil sedemikian rupa agar ber­gerak ke arah optimum atau sekitar optimum pada permukaan respon. Karena eksperimen berikutnya kita harapkan harus ber­gerak dalam arah mendaki paling cepat menuju titik optimum atau dekat sekitar optimum pada permukaan respon, maka metoda ini dinamakan lintas pendakian tercuram. Teknik ini tidak menentu­kan berapa jauh eksperimen berikutnya dilakukan dari eksperimen awal, namun cukup mengatakan kepada pelaksana arah mane eksperimen berikutnya harus dilaksanakan.

Untuk menentukan persamaan permukaan respon, beberapa desain atau model telah dirumuskan agar dengan menggunakan eksperimen sesedikit mungkin persamaan tersebut dapat didekati. Dalam hal berdimensi dua, untuk permukaan respon yang paling sederhana persamaan atau modelnya adalah

Y = B₀ X₀ + B₁ X₁ + B₂ X₂ +

Dengan pengertian Y respon, X₀ harganya selalu diambil satu, X₁ dan X₂ masing-masing prediktor, B₀, B₁ dan B₂ nantinya ditaksir menggunakan metoda kuadrat terkecil sehingga meminimalkan jumlah kuadrat-kuadrat kekeliruan .

Model di atas biasa disebut iersarnaan order pertama meng­ingat pangkat prediktor (X₁ dan X₂) besarnya satu.

Jika karena sesuatu kejelasan model permukaan respon tidak berorder satu seperti di atas (untuk dua dimensi), maka mungkin harus diambil model berorder dua yang bentuk umumnya

Y = B₀,X₀ + B₁ X₁ + B₂ X₂ + B₁₁, + B₁₂ X ₁X₂ + B₂₂X +

Dengan pengertian tiap lambang seperti dijelaskan di atas dengan perluasan seperlunya. Suku X₁X₂ menunjukkan interaksi antara variabel-variabel X₁ dan X₂.

Untuk keadaan berdimensi tiga, yakni respon Y melibatkan. ti­ga prediktor X₁, X₂ dan X_3, model permukaan respon berorder satu adalah

Y = B₀X₀ + B₁X₁ + B₂X₂ + B₃X₃ +

Yang biasa disebut bidang hyper. Model berorder duanya adalah

Y = B₀X₀ + B₁X₁ + B₂X₂ + B₃X₃ + B₁₁ + B₂₂

+ B₃₃ + B₁₂X₁ X₂ + B₁₃X₁ X₃ + B₂₃ X₂ X₃ +

Dengan interaksi-interaksi antara X₁ dan X₂, X₁dan X_3, X₂ dan X₃

Semua koefisien B dalam model-model di atas, nantinya ditak­sir menggunakan metoda kuadrat terkecil berdasarkan data hasil eksperimen.

Mudah dimengerti kiranya, bahwa makin banyak variabel bebas yang terlibat kepada respon, makin kompleks modelnya dan makin sulit menentukan harga-harga taksiran koefisien-koefisien dalam model.

Pertanyaannya sekarang adalah: “Bagaimana koefisien-koefisi­en B dalam suatu model ditaksir?”

Ambil model Y = B₀ X₀ + B₁ X _I + B₂ X₂ + . Karena ada tiga parameter yang harus ditaksir, ialah B₀ B₁ dan B₂ maka paling sedikit diperlukan tiga titik eksperimen. Desain yang diperlukan bisa berupa segitiga samakaki. Akan tetapi karena eksperimen me­libatkan dua faktor X₁ dan X₂, maka masing-masing faktor dapat dibuat dua taraf sehingga bisa digunakan desain faktorial 2² berupa desain bujursangkar yang sudut-sudutnya dibentuk oleh titik-titik

X₁ taraf rendah dan X₂ taraf rendah

X₁ taraf rendah dan X₂ taraf tinggi

X₁ taraf tinggi dan X₂ taraf rendah

X₁ taraf tinggi dan X₂ taraf tinggi.

Atau (lihat Bag. VI.2, Bab VI) bujursangkar tersebut dibentuk oleh titik-titik (1), a, b dan ab.

Untuk menaksir B₀, B₁ dan B₂ sehingga nantinya diperoleh bidang perkiraan terbaik, seperti telah disebutkan, menggunakan metoda kuadrat terkecil. Dengan meminimalkan jumlah kuadrat kekeliruan , yakni :

menggunakan hitung diferensial akan diperoleh sistem persamaan normal.

Untuk harga-harga data eksperimen yang diketahui, sistem persamaan XVI (1) akan menghasilkan b₀, b₁, dan b₂ yang ma­sing-masing sebagai taksiran bagi Bo, B₁, dan B₂.

Sistem persamaan di atas cukup memakan waktu untuk dise­lesaikan sehingga sebaiknya digunakan bantuan komputer. Ban­tuan komputer ini akan makin terasa diperlukan untuk model order tinggi dan jugs untuk model yang melibatkan banyak prediktor.

Akan tetapi dengan mengambil X₁, dan X₂ sebagai fungsi dari variabel eksperimen yang cocok kita dapat menyusun X, dan X2 menjadi berharga -1 atau + 1 sehingga sistem persamaan XVI (1) sangat disederhanakan dan X₁, dan X₂, membentuk sistem orto­gonal, yakni bahwa EX₁ = EX₂ = 0 dan = 0

Akibat adanya sistem ortogonal ini, maka sistem persamaan normal XVI (1) berubah menjadi sebagai berikut.

Untuk menguji keberartian tiap koefisien perlu dicari jumlah kuadrat-kuadrat JK tiap koefisien yang dapat dihitung mengguna­kan :

XVI(3) ... JK (b_i ) = b_i . ∑ X_i Y

yang masing-masing memiliki derajat kebebasan satu.

Contoh.

Perhatikan semacam, plastik tembus pandang yang akan di­semprot menggunakan penyemprot jenis tertentu dengan hasil semprotan masih tetap membuat plastik itu tembus pandang. Semprotan mempunyai konsentrasi zat warna yang dipilih (X₁) sedangkan plastik disemprot pada posisi (X₂ ) tertentu. Lapisan sebagai hasil semprotan akan mengurangi daya pan­dang apabila lapisan itu makin tebal.

Eksperimen dilakukan dengan tujuan warna permukaan plas­tik seperti warna yang dipilih tadi tetapi daya pandang harus maksimum. Ini mengundang untuk mencari eksperimen perta­ma sedemikian agar ditemukan arch eksperimen berikutnya yang secepat mungkin menuju maksimum terjadinya daya pandang. Masalah ini tidak lain daripada lintas pendakian ter­curam.

Dengan memisalkan permukaan berbentuk bidang pada daerah yang kecil, maka eksperimen pertama digunakan untuk menentu­kan persamaan bidang ini. Permukaan respon memiliki persamaan berbentuk umum

Y = B₀X₀ + B₁X₁ + B₂X₂

Karena ada tiga parameter yang perlu ditaksir, seperti telah dijelas­kan kita bentuk desain faktorial 2² ; jadi X₁, dan X₂, masing-masing dibuat menjadi dua taraf. Misalkan untuk eksperimen pertama di­sepakati X₁, diambil konsentrasi (K) pads 10% dan 14% sedangkan X₂ diambil posisi (P) mendatar atau 0^o dan vertikal atau 90°. Res­pon Y adalah daya pandang diukur dengan satuan tertentu. Eksperimen dilakukan menggunakan DAS tanpa replikasi dan misalkan diperoleh hasil seperti berikut.

Y	K	P	X1	X2
9,5 7,9 9,6 9,4	10% 10% 14% 14%	0O 90O 0O 90O	-1 -1 +1 +1	-1 +1 -1 +1

Dengan mengambil X₁mudah dicek bahwa diperoleh harga-harga X₁ dan X₂ berbentuk -1 atau +1 seperti telah dicantumkan dalam daftar itu. Secara grafik, data dalam daftar itu dapat dilihat seperti dalam Gambar XVI (3).

Untuk menentukan koefisien-koefisien bidang kita buat daftar berikut agar mudah dipelajari.

Menggunakan Rumus XVI (2) diperoleh

b_o = 36,4/4 = 9,10

b1 = 1,6/4 = 0,40

b2 = -1,8/4 = -0,45

sehingga persamaan bidang adalah :

Ỷ = 9,10 + 0,40 X₁ – 0,45 X₂

untuk menentukan arah eksperimen yang harus dilakukan berikutnya, digambarkan kontur untuk respon yang sama menggunakan persamaan bidang di atas.

(yakni Ỷ = 9,10 + 0,40 X₁ – 0,45 X₂)

Nyatakan X₂ oleh X₁, maka

X₂ =

Jika Y = 7,5, maka X₂ =

Dan untuk

X₁ = -1 → X₂ = 2,67

X₁ = +1 → X₂ = 4,44

Jika Y = 8,0, maka X₂ =

Dan untuk

X₁ = -1 → X₂ = 1,56

X₁ = +1 → X₂ = 3,33

Jika Y = 8,5, maka X₂ =

Dan untuk

X₁ = -1 → X₂ = 0,44

X₁ = +1 → X₂ = 2,22

Jika Y = 9,0, maka X₂ =

Dan untuk

X₁ = -1 → X₂ = - 0,67

X₁ = +1 → X₂ = 1,11

Jika Y = 9,5, maka X₂ =

Dan untuk

X₁ = -1 → X₂ = -1,78

X₁ = +1 → X₂ = 0,00

Hasil perhitungan di atas, dirangkum dalam daftar berikut.

Kelima buah titik dalam daftar di atas menghasilkan kontur seperti dalam Gambar XVI (4) yang merupakan garis-garis sejajar.

Dari grafik dapat dilihat bahwa Y yang menuju ke harga optimum arahnya ke sudut kanan bawah. Dengan menelusuri garis normal pada kontur-kontur dan bergerak ke atas menuju permukaan, kita akan memperoleh respon yang besar sehingga mencapai puncaknya. Kita perhatikan persamaan normal (pada kontur-kontur) yang melalui titik asal (0,0). Karena kontur-kontur memiliki persamaan.

Dengan koefisien arah 0,40/0,45 = 8,19, maka garis normal akan mempunyai koefisien arah (-9/8); sehingga normal yang melalui titik asal mempunyai persamaan.

(Dalam grafik dinyatakan dengan anak panah).

Garis normal ini memberikan arah melakukan eksperimen berikutnya (seperti telah disebutkan, tidak menyebutkan berapa jauh eksperimen ditempuh dalam arah ini). Dengan adanya arah ini, eksperimen berikut bisa dilakukan dengan pusat faktorial pada titik (+1, -9/8) yang menghasilkan keempat buah titik eksperimen berikut.

````

Gambar XVI (5) melukiskan bujursangkar eksperimen yang baru dengan pusat (+1, - 9/8 ). Tampak bahwa bujursangkar eksperi­men ini bergeser ke kanan bawah bila dibandingkan dengan bujur­sangkar eksperimen pertama dengan pusat (0,0). Pergeseran inj dikarenakan normal pada kontur-kontur yang dijelaskan di muka.

Keempat titik eksperimen kedua di atas kita terjernahkan ke variabel eksperimen (ialah konsentrasi clan posisi) dengan menggunakan

X<sub>1</sub> = atau K = 2 X<sub>1</sub> + 12

X<sub>2</sub> = atau K = 45 (X<sub>2</sub> + 1)

Menggunakan variabel eksperimen K dan P ini, maka eempat titik eksperimen yang baru adalah :

Eksperimen kedua dilakukan menggunakan konsentrasi 12% dan 16% sedangkan posisi yang digunakan adalah 39,4° menyudut ke atas dengan garis datar dan 50,6° menyudut ke bawah dengan ga­ris datar. Lakukan eksperimen faktorial 2<sup>2</sup> dengan keadaan tersebut, (jika eksperimen seperti itu dapat dilaksanakan) catat res­ponnya dan lakukan analisis ter`` hadap data yang diperoleh untuk menentukan arch eksperimen yang baru lagi. Prosedur ini terns dilakukan hingga akhirnya diperoleh respon optimum atau sekitar optimum yang dikehendaki.

Marilah kita periksa keberartian koefisien model yang diper­oleh dari eksperimen pertama. Menggunakan Rumus XVI (3) di­peroleh jumlah kuadrat-kuadrat

JK (b<sub>0</sub>) = (9,10)(36,4) = 331,24

JK (b<sub>1</sub>) = (0,40)(1,6) = 0,64

JK (b<sub>2</sub>) = (-0,45)(-1,8) = 0,81

Dan JK(total) = 9,5<sup>2</sup> + 7,9<sup>2</sup> +9,6<sup>2</sup> +9,4<sup>2</sup>

= 333,18

Disusun dalam daftar ANAVA diperoleh seperti berikut.

DAFTAR XVI (1)
DAFTAR ANAVA PERMUKAAN RESPON
CONTOH FAKTORIAL 2<sup>2</sup>

Dengan hanya dk = 1 untuk residu atau sisa, tidak ada tes yang baik untuk meneliti keberartian koefisien-koefisien dalam model dan tentunya juga tidak bisa diperoleh informasi berapa baik bi­dang dapat mendekati permukaan respon.

Salah satu usaha yang bisa dilakukan untuk mengatasi ini de­ngan jalan mengambil dua atau lebih titik di pusat bujursangkar eksperimen. Dengan melakukan replikasi pada titik yang sama. taksiran galat eksperimen bisa diperoleh dan rata-rata respon pada titik pusat memberikan taksiran kecocokan bidang.

Sekarang, mari kita ambil dua titik di pusat bujursangkar eksperimen yang jika digabungkan dengan eksperimen pertama diperoleh data berikut.

Dari data diatas dihasilkan :

X<sub>0</sub> Y = 54,8 X<sub>1</sub> Y = 1,6

X<sub>2</sub> Y = -1,8 X Y = 4

X Y = 4 dan n = 6

Sehingga dengan Rumus XVI (3) diperoleh :

b<sub>o</sub> = 54,8/6 = 9,13

b<sub>1</sub> = 1,64/4 = 0,40

b<sub>2</sub> = -1,8/4 = - 0,45

Sedangkan jumlah kuadrat-kuadratnya

JK (Bo) = (9,13) (54,8) = 500,32

JK (B1) = (0,40) (1,6) = 0,64

JK (B2) = (-0,45) (-1,8) = 0,81

JK (Total) = 502,93

JK (Galat di titik (0,0) = pusat) =

= (9,1)<sup>2</sup> + (9,3)<sup>2</sup> -

Harga-harga di atas menghasilkan daftar ANAVA berikut :

JK (Residu) = JK (Total) – JK (b<sub>o</sub>) – JK (b<sub>1</sub>) – JK (b<sub>2</sub>)

= 502,93 – 500,32 – 0,64 -0,81 = 1,16

Dengan dk = 6 – 1 – 1 – 1 = 3

JK (Residu) ini dipecah menjadi JK (Galat) dan JK (Kecocokan). Karena JK (Galat) = 0,02 maka JK (Kecocokan) = 1,14

Semua uji dilakukan terhadap galat, jadi dipeoleh :

Untuk b<sub>o</sub> : F =

Untuk b<sub>1</sub> : F =

Untuk b<sub>2</sub> : F =

Kecocokan : F =

Dengan hanya melakukan dua eksperimen di titik pusat dua kali, tampak bahwa derajat kebebasan untuk residu telah berubah menjadi tiga, sehingga galat dan kecocokan bisa diperoleh. Dari daftar ANAVA dengan harga-harga statistik F dihitung di atas, ha­nya koefisien b<sub>o</sub> yang signifikan (pada taraf nyata 0,05) sedangkan lainnya tidak termasuk kecocokan bidang. Namun demikian, sta­tistik F untuk koefisien-koefisien lebih besar dari statistik F untuk kecocokan. Ini menunjukkan bahwa bidang

Y = 9,13 + 0,40 X<sub>1</sub> - 0,45 X<sub>2</sub>

merupakan pendekatan yang wajar terhadap bidang respon meng­gunakan eksperimen pertama dengan dua titik pusat.

XVI.5 SOAL-SOAL

1. Jelaskan apa yang dimaksud dengan permukaan respon suatu eksperimen.

2. Bagaimana atau apa bentuk permukaan respon jika dalam eksperimen itu hanya ada satu prediktor? Bagaimana jika ada dua, tiga dan empat prediktor?

4. Apa yang dimaksud dengan kontur untuk suatu eksperimen?

5. Jelaskan kegunaan permukaan respon suatu eksperimen.

6. Uraikan langkah-langkah metoda lintas pendakian tercuram.

7. Lihat kembali daftar ANAVA dalam Daftar XVI (2). Jika uji kecocokan signifikan atau sangat signifikan, apa yang harus di­lakukan?

8. Perhatikan kembali contoh yang dijelaskan dalam teks. Laku­kan analisnya sekarang terhadap eksperimen faktorial 2<sup>2</sup> te­tapi menggunakan lima titik di pusat eksperimen dengan data berikut.

4. Seorang insinyur kimia bermaksud menentukan kondisi proses yang memberikan hasil proses maksimum. Untuk itu ia mengadakan eksperimen dengan mengambil dua variabel kontrol ialah waktu reaksi dan temperatur reaksi. Sekarang ia melakukan proses dengan menggunakan waktu reaksi 35 menit dan temperatur reaksi 155°F yang memberikan hasil proses sekitar 40%. la ingin menggunakan metoda lintas pen­dakian tercuram dan mengambil model order satu dalam rangka meneliti tercapainya proses maksimum. Ditentukan bahwa untuk itu dapat diambil waktu reaksi 30 menit dan 40 menit sedangkan temperatur reaksi 150°F dan 160°F Dari eksperimen yang dilakukan diperoleh respon Y berikut.

Bagaimana hasil eksperimen ini?

BAB XVII
OPERASI EVOLUSIONER (OPEV)

XVII.1 PENDAHULUAN

Metoda permukaan respon sering digunakan oleh bagian riset dan pengembangan dalam pilot project suatu pabrik. Apabila diterapkan pada proses produksi berskala penuh biasanya hanya sekali saja (atau sangat jarang) karena prosedur eksperimennya cukup harus terinci dan teliti. Tambahan pula, kondisi yang ter­capai optimum pada pilot project bisa tidak terjadi optimum pada produksi berskala penuh.

Untuk mengatasi hal ini, suatu metoda, dikenal dengan na­ma operasi evolusioner disingkat OPEV, diusulkan oleh Box [4] dengan nama evolutionary operation disingkat EVOP.

XXII.2 OPERASI EVOLUSIONER (OPEV)

Metoda operasi evolusioner (OPEV) adalah metoda yang dirancang untuk digunakan dalam proses yang berjalan atau ber­operasi secara rutin di perusahaan dengan tujuan meningkatkan produktivitas. Jadi metoda ini kegiatannya melekat dalam proses yang dilaksanakan oleh karyawan dengan bantuan seminimum mungkin dari bagian penelitian atau pengembangan diperusahaan itu. Metoda ini berhasil baik untuk kondisi proses yang tidak mengalami perubahan besar atau mendadak yang<sup>-</sup>mungkin meng­ganggu atau mengacaukan produksi.

Prosedur OPEV terdiri dari pelaksanaan sebuah eksperimen sederhana, biasanya berupa faktorial 2<sup>k</sup> , dalam lingkup proses yang sedang berlangsung. Perubahan dalam variabel-variabel di­misalkan cukup kecil sehingga gangguan-gangguan yang berarti atau serius terhadap hasil, kualitas atau kuantitas tidak akan terjadi. Dari eksperimen yang dilakukan, data dikumpulkan un­tuk variabel respon, biasanya hasil produk, pada berbagai titik atau kombinasi perlakuan desain eksperimen. Apabila satu set data telah diperoleh dari semua titik desain eksperimen atau telah diambil satu pengamatan pada tiap titik desain, maka dikatakan bahwa satu siklus telah terjadi. Biasanya satu siklus sering tidak cukup untuk melihat terjadinya pergeseran dalam harga-harga respon, karena itu siklus kedua perlu diambil. Jika perlu diambil lagi siklus berikutnya sehingga efek-efek sebuah atau lebih va­riabel kontrol, interaksinya terhadap variabel respon ataupun perubahan dalam rata-rata tampak signifikan dibandingkan terhadap ukuran galat eksperimen. Setelah berhasil ditemukan pertambahan hasil produk secara signifikan, dikatakan bahwa satu fase telah terjadi dan pada saat inilah biasanya keputusan dibuat untuk mengubah kondisi-kondisi dasar kerja proses ke arah perbaikan atau meningkatkan respon (hasil produk).

Untuk menguji variabel-variabel proses ikontrol) dan inter­aksinya, seperti dapat disinipulnan dari uraian di atas, diperlukan taksiran galat eksperimen yang diperoleh dari data siklus. Lagi pula, desain faktorial 2<sup>k</sup> biasanya terpusat sekitar kondisi ope­rasional proses paling baik yang sekarang berlangsung. Dengan jalan membandingkan respon pada titik terbaik (optimum) ini dengan respon pada titik-titik lainnya dalam faktorial 2<sup>k</sup> kita bisa mencek perubahan dalam rasa-rasa respon. Jika proses me­mang telah terpusat pada titik maksimum maka respon pada titik itu harus secara signifikan lebih besar dari respon-respon pada titik-titik desain 2<sup>k</sup> lainnya.

Dalam teori, OPEV dapat digunakan untuk k buah variabel proses, namun dalam prakteknva biasanya hanya digunakan untuk dua atau tiga variabel saja.

Contoh.:

Seorang insinyur i~imia mempelajari bahwa hasil suatu proses melibatkan temperatur (X<sub>1</sub> ) dan tekanan (X<sub>2</sub> ). Kondisi ke­dua faktor itu pada saat proses yang sekarang berlangsung adalah: temperatur 250°F dan tekanan 145 kg/cm<sup>2</sup>. Prosedur OPEV menggunakan empat titik desain faktorial 2<sup>2</sup> ditambah satu titik pusat dengan kondisi berikut.

Satu siklus terjadi secara lengkap dengan jalan melaksanakan proses pada kelima titik, secara berurutan : (1), (2), (3), (4), dan (5) masing-masing satu kali.

Untuk mempelajari hasil suatu siklus, biasanya data disajikan dalam lembar OPEV yang bentuknya untuk siklus pertama ini tampak seperti dalam daftar XVII (1).

Karena baru siklus pertama, jelas butir-butir (i), (ii) dan aki­batnya (iv) belum terisi. Demikian pula semua butir untuk per­hitungan simpangan baku dan batas galat. Bilangan-bilangan di ba­wah perhitungan efek-efek, diperoleh berdasarkan hal-hal berikut.

efek temperatur : rata-rata pada titik (3) dan (4) dibandingkan dengan rata-rata pada titik (2) dan (5).

efek tekanan : rata-rata pada titik (3) dan (5) dibandingkan dengan rata-rata pada titik (2) dan (4).

efek interaksi : rata-rata pada titik (2) dan (3) dibandingkan dengan rata-rata pada titik (4) dan (5).

Perubahan dalam rata-rata: respon pada titik-titik (2), (3), (4) dan (5) dibandingkan dengan respon pada titik (1).

Di bawah kolom perhitungan simpangan baku, mudah dilihat bah­wa berdasarkan siklus pertama ini sudah ada taksiran untuk sim­pangan baku sehingga dari daftar untuk siklus ini tidak banyak informasi yang diperoleh. Karena itu diperlukan siklus kedua. Sementara itu, untuk menghitung s baru diperlukan koefisien f<sub>k</sub>,<sub>n</sub> dengan pengertian k = banyak titik desain dan n = banyak siklus. Koefisien-koefisien itu untuk beberapa harga k dan n di­berikan di bawah ini.

Perhitungan batas galat menggunakan koefisien kepercayaan 95 % sehingga galat baku rata-rata dan galat baku efek besarnya sedangkan galat baku perubahan dalam rata-rata, untuk koefisien kepercayaan yang sama, adalah

Y : 79,9 79,6 80,9 78,5 79,0

Ambil sekarang siklus kedua dan misalkan hasilnya pada tiap titik yang sama, diperoleh data berikut :

Masukkan data baru ini bersama-sama dengan data siklus per­tama ke dalam lembar OPEV dan lakukan perhitungan yang di­perlukan. Diperoleh lembar OPEV untuk n = 2 seperti dalam Daf­tar XVII (3).

Dari Daftar XVII (2) untuk siklus n = 2 tampak bahwa semua perhitungan dalam kolom perhitungan harga rata-rata dengan mu­dah dapat dilakukan sesuai dengan petunjuk yang ada di sebelah kirinya. Semua perhitungan efek menggunakan data rata-rata baru dalam butir (vi).

Dalam kolom perhitungan simpangan baku, tampak bahwa jumlah s dan rata-rata s sebelumnya masih belum terisi, karena ke­dua-duanya diisikan dari siklus pertama yang harga-harganya be­lum ada. Rentang dari (iv) diperoleh dengan jalan mengurangi data terbesar (+1,0) oleh data terkeeil ( -1,0); hasilnya (+1,0) - ( -1,0) = 2,0. Adapun s baru = (2,0) x (0,30) = 0,60 (dari Daf­tar XVII (2) f<sub>k</sub>,<sub>n</sub> untuk k = 5 adalah f<sub>k</sub>,<sub>n</sub> = 0,30), sehingga jum­lah s baru = s siklus kedua ditambah s siklus pertama yang belum ada = 0,60 dan akibatnya rata-rata s baru = 0,60 / (2 - 1) = 0,60 Rata-rata s baru ini digunakan untuk menghitung batas-batas galat van,- hasilnya dapat dilihat dalam Daftar XVII (3).

Karena dari Daftar XVII (3) kita baca tidak ada efek yang har­ga-harganya lebih besar dari batas-batas galat, ini berarti efek se­benarnya barangkali nol. Ini mengundang kita untuk mengambil siklus ketiga.

Misalkan siklus ketiga memberikan hasil berikut (untuk titik desain yang sama seperti di siklus pertama dan kedua).

Y : 79,9 79,6 80,9 78,5 79,0

Setelah dimasukkan ke dalam lembar OPEV menggunakan lembar OPEV siklus kedua, diperoleh daftar XVII (4).

Dari daftar XVII (4) itu dapat dilihat bahwa efek tekanan (0,865) adalah signifikan karena lebih besar dari batas galatnya (0,670) dan efek temparatur (0,665) = 0,67 sama dengan batas galat rata-rata (0,670).

Sekali ada efek yang signifikan, maka prosedur OPEV fase pertama telah selesai/terjadi secara lengkap.

Hasil fase pertama ini sudah mengusulkan kepada kita untuk mengadakan perubahan kondisi proses dan langkah itu dibenarkan. Dari hasil-hasil OPEV fase pertama, cukup beralasan jika untuk OPEV fase kedua digunakan titik pusat (3) ialah pada temparatur 255<sup>o</sup>F dan tekanan 150 kg/cm<sup>2</sup>, sedangkan desainnya tetap desain faktorial 2<sup>2.</sup>

Hasil OPEV memberikan masukan kepada operator dan peng­awas proses. Agar masukan ini mudah digunakan, biasanya dibuat papan OPEV yang berisikan informasi pokok yang diperoleh dari OPEV fase yang selesai. Untuk hash OPEV fase pertama dalam contoh kita, papan OPEV berbentuk seperti pada Daftar XVII (5).

XVII.3 SOAL - SOAL

1. Jelaskan kelebihan prosedur OPEV dibanding dengan prosedur permukaan respon.

2. Jelaskan bagaimana prosedur OPEV biasanya dilaksanakan.

3. Apakah yang dimaksud dengan siklus dan apa pula fase yang dikenal dalam prosedur OPEV?

4. Pelajari kembali lembar Perhitungan OPEV. Unsur-unsur apa saja yang digunakan dan perlu dihitung?

5. Hal apa saja yang dicantumkan dalam Papan Informasi OPEV dan untuk apa kegunaannya?

6. Hasil proses. kimia untuk empat siklus pertama diberikan di bawah ini. Variabel-variabel yang digunakan adalah persentase konsentrasi (X, ) pada taraf 20, 21 dan 22 dan temperatur proses (X<sub>2</sub>) pada taraf 130<sup>o</sup>, 132<sup>o</sup> dan 134°F.

1. Lakukan analis terhadap data di atas menggunakan metoda OPEV dan berikan kesimpulan.

2. Buat papan informasi OPEV berdasarkan hasil analisis tersebut.